Kelompok Besaran Di Bawah Ini Yang Merupakan Kelompok Besaran Turunan Adalah

As we delve into the topic of kelompok besaran di bawah ini yang merupakan kelompok besaran turunan adalah, it’s essential to understand the concept of derived quantities. Derived quantities are those that are formed by combining base quantities using mathematical operations like multiplication, division, or exponentiation. These derived quantities are crucial in physics and other scientific disciplines as they provide a way to express complex relationships between different physical properties.

In the realm of measurement units, derived quantities play a significant role in simplifying calculations and representing physical phenomena accurately. By deriving new quantities from base units such as length, mass, time, electric current, temperature, amount of substance, and luminous intensity, scientists can create a more comprehensive framework for understanding the natural world.

When identifying which groups below constitute derived quantity groups, one must consider how these measurements interact with each other based on established principles and formulas Kelompok Besaran Di Bawah Ini Yang Merupakan Kelompok Besaran Turunan Adalah. Through this analysis, we can distinguish between base quantities and their derivatives to gain insight into the interconnected nature of various physical parameters. By recognizing these relationships, we can further our comprehension of fundamental laws governing the universe.

Understanding Derived Quantities

Exploring the realm of derived quantities opens up a fascinating world where measurements are intertwined with complex relationships. These quantities are NOT fundamental but are derived from fundamental base quantities through mathematical operations or formulae. Imagine unraveling the intricacies of physical phenomena and expressing them in terms of these interconnected derived units.

One key aspect to grasp is that derived quantities Kelompok Besaran Di Bawah Ini Yang Merupakan Kelompok Besaran Turunan Adalah do not stand alone; they depend on fundamental units for their existence. This interdependence highlights how various aspects of the physical world are inherently linked, emphasizing the unity within diversity concept prevalent in science. By understanding how these derived quantities evolve from basic measurements, we gain a deeper appreciation for the underlying principles governing our universe.

Derived quantities find applications across diverse fields, from physics and engineering to economics and social sciences. They serve as essential building blocks for formulating laws, equations, and models that describe natural phenomena. Through meticulous calculations involving derived units, scientists and researchers can predict outcomes, analyze trends, and make informed decisions based on quantitative data.

To illustrate the significance of derived quantities Kelompok Besaran Di Bawah Ini Yang Merupakan Kelompok Besaran Turunan Adalah, let’s consider an example from mechanics: velocity. Velocity is a DERIVED quantity obtained by dividing displacement by time. This simple yet powerful relationship encapsulates the essence of derived units – they provide valuable insights into motion dynamics while relying on fundamental measurements like distance and time.

In essence, delving into derived quantities unveils a structured framework through which we can comprehend complex systems and phenomena in a quantifiable manner. By recognizing the interconnectedness between base units and their derivatives, we enhance our ability to interpret data effectively, solve intricate problems, and advance scientific knowledge across various disciplines.

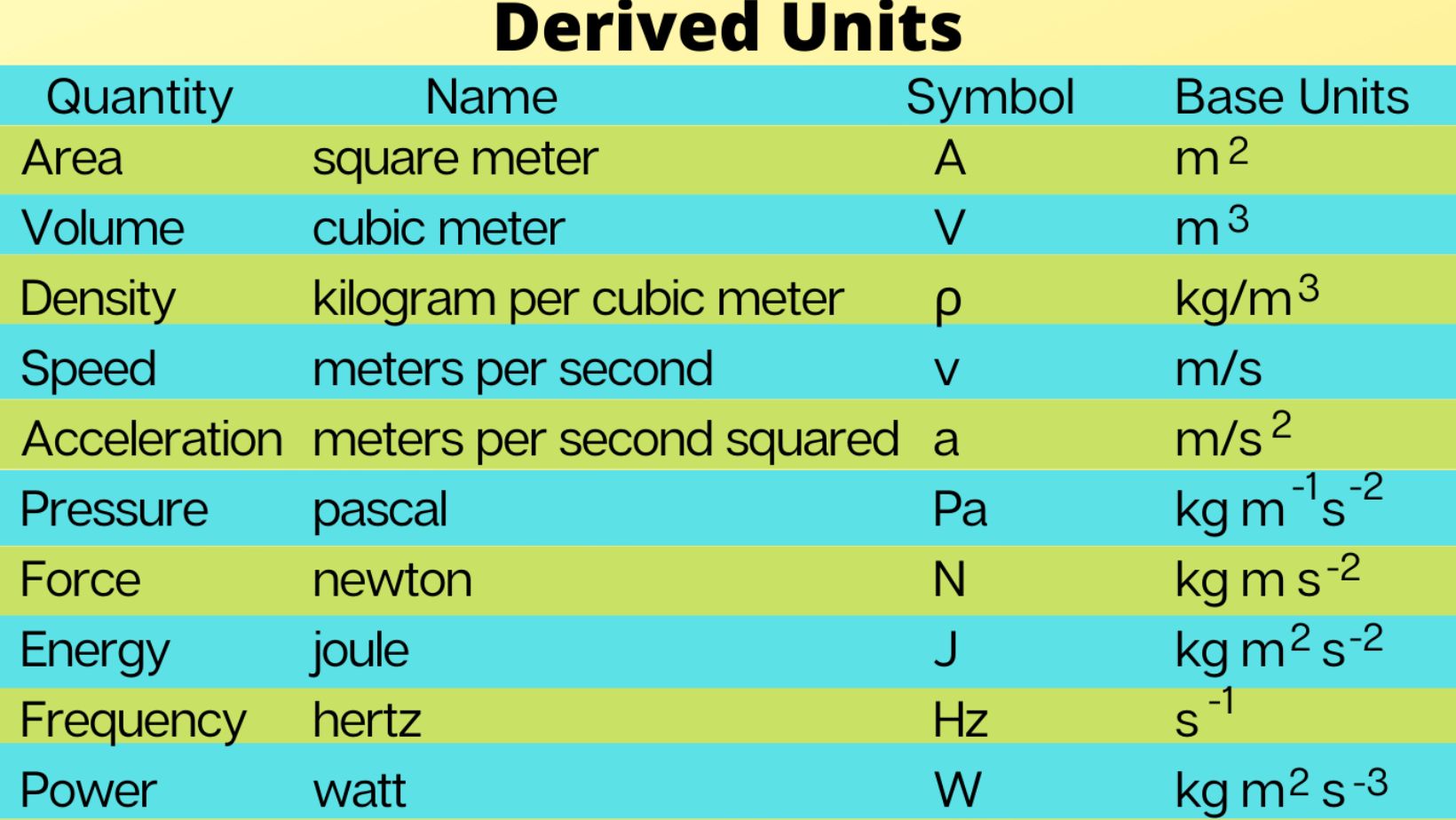
Examples of Derived Quantities

In the realm of physics, derived quantities play a pivotal role in expanding our understanding of fundamental measurements. These quantities are intricately linked to base units but are formed through mathematical combinations or transformations. Let’s delve into some concrete examples to grasp their significance.

Speed

Speed is a classic example of a derived quantity, defined as the distance traveled per unit time. It’s calculated by dividing the distance covered by an object with the time taken to cover that distance. The SI unit for speed is meters per second (m/s), showcasing its derived nature from fundamental units of length and time.

Acceleration

Acceleration exemplifies another crucial derived quantity that describes how velocity changes over time. It’s computed by dividing the change in velocity by the time taken for that change. In SI units, acceleration is measured in meters per second squared (m/s²), underscoring its derivation from basic units of length and time.